机器学习常用术语
机器学习是一门专业性很强的技术,它大量地应用了数学、统计学上的知识,因此总会有一些蹩脚的词汇,这些词汇就像“拦路虎”一样阻碍着我们前进,甚至把我们吓跑。因此认识,并理解这些词汇是首当其冲的任务。本节将介绍机器学习中常用的基本概念,为后续的知识学习打下坚实的基础。
模型这一词语将会贯穿整个教程的始末,它是机器学习中的核心概念。你可以把它看做一个“魔法盒”,你向它许愿(输入数据),它就会帮你实现愿望(输出预测结果)。整个机器学习的过程都将围绕模型展开,训练出一个最优质的“魔法盒”,它可以尽量精准的实现你许的“愿望”,这就是机器学习的目标。

图1:样本&特征
由上图可知数据集的构成是“一行一样本,一列一特征”。特征值也可以理解为数据的相关性,每一列的数据都与这一列的特征值相关。
第一个常用术语就是“向量”,向量是机器学习的关键术语。向量在线性代数中有着严格的定义。向量也称欧几里得向量、几何向量、矢量,指具有大小和方向的量。您可以形象地把它的理解为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量只有大小,没有方向。
在机器学习中,模型算法的运算均基于线性代数运算法则,比如行列式、矩阵运算、线性方程等等。其实对于这些运算法则学习起来并不难,它们都有着一定运算规则,只需套用即可,因此你也不必彷徨,可参考向量运算法则。向量的计算可采用 NmuPy 来实现,如下所示:
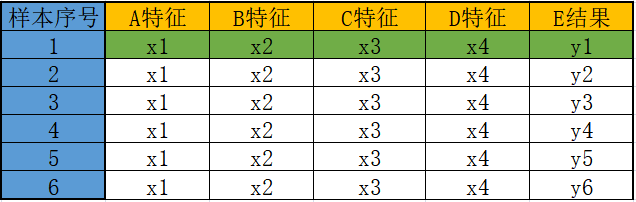
图2:矩阵表格
如果用二维矩阵的表示的话,其格式如下所示:

假设函数和损失函数是机器学习中的两个概念,它并非某个模块下的函数方法,而是我们根据实际应用场景确定的一种函数形式,就像你解决数学的应用题目一样,根据题意写出解决问题的方程组。下面分别来看一下它们的含义。

图3:函数关系图
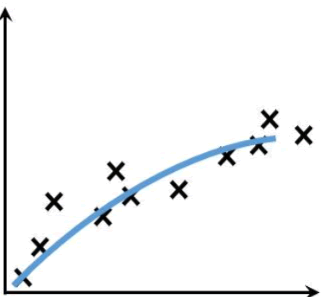
图4:曲线拟合
举一个简单的例子,比如你训练一个识别狗狗照片的模型,如果你只用金毛犬的照片训练,那么该模型就只吸纳了金毛狗的相关特征,此时让训练好的模型识别一只“泰迪犬”,那么结果可想而知,该模型会认为“泰迪”不是一条狗。如下图所示:

图5:过拟合
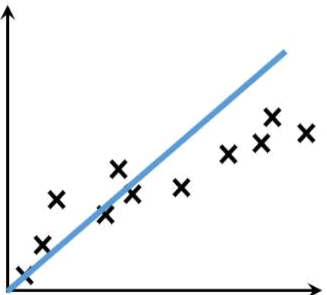
图6:欠拟合
造成欠拟合的主要原因是由于没有选择好合适的特征值,比如使用一次函数(y=kx+b)去拟合具有对数特征的散落点(y=log2x),示例图如下所示:
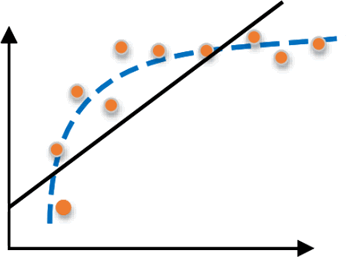
图7:欠拟合示例图
欠拟合和过拟合是机器学习中会遇到的问题,这两种情况都不是我期望看到的,因此要避免,关于如何处理类似问题,在后续内容中还会陆续讲解,本节只需要大家熟悉并理解常见的机器学习术语和一些概念即可。
机器学习术语
1) 模型模型这一词语将会贯穿整个教程的始末,它是机器学习中的核心概念。你可以把它看做一个“魔法盒”,你向它许愿(输入数据),它就会帮你实现愿望(输出预测结果)。整个机器学习的过程都将围绕模型展开,训练出一个最优质的“魔法盒”,它可以尽量精准的实现你许的“愿望”,这就是机器学习的目标。
2) 数据集
数据集,从字面意思很容易理解,它表示一个承载数据的集合,如果说“模型”是“魔法盒”的话,那么数据集就是负责给它充能的“能量电池”,简单地说,如果缺少了数据集,那么模型就没有存在的意义了。数据集可划分为“训练集”和“测试集”,它们分别在机器学习的“训练阶段”和“预测输出阶段”起着重要的作用。3) 样本&特征
样本指的是数据集中的数据,一条数据被称为“一个样本”,通常情况下,样本会包含多个特征值用来描述数据,比如现在有一组描述人形态的数据“180 70 25”如果单看数据你会非常茫然,但是用“特征”描述后就会变得容易理解,如下所示:
图1:样本&特征
4) 向量
任何一门算法都会涉及到许多数学上的术语或者公式。在本教程写作的过程中也会涉及到很多数学公式,以及专业的术语,在这里我们先对常用的基本术语做一下简单讲解。第一个常用术语就是“向量”,向量是机器学习的关键术语。向量在线性代数中有着严格的定义。向量也称欧几里得向量、几何向量、矢量,指具有大小和方向的量。您可以形象地把它的理解为带箭头的线段。箭头所指:代表向量的方向;线段长度:代表向量的大小。与向量对应的量叫做数量(物理学中称标量),数量只有大小,没有方向。
在机器学习中,模型算法的运算均基于线性代数运算法则,比如行列式、矩阵运算、线性方程等等。其实对于这些运算法则学习起来并不难,它们都有着一定运算规则,只需套用即可,因此你也不必彷徨,可参考向量运算法则。向量的计算可采用 NmuPy 来实现,如下所示:
import numpy as np #构建向量数组 a=np.array([-1,2]) b=np.array([3,-1]) #加法 a_b=a+b #数乘 a2=a*2 b3=b*(-3) #减法 b_a=a-b print(a_b,a2,b3,b_a)输出结果:
[2 1] [-2 4] [-9 3] [-4 3]简而言之,数据集中的每一个样本都是一条具有向量形式的数据。
5) 矩阵
矩阵也是一个常用的数学术语,你可以把矩阵看成由向量组成的二维数组,数据集就是以二维矩阵的形式存储数据的,你可以把它形象的理解为电子表格“一行一样本,一列一特征”表现形式如下:
图2:矩阵表格

假设函数&损失函数
机器学习在构建模型的过程中会应用大量的数学函数,正因为如此很多初学者对此产生畏惧,那么它们真会有这么可怕吗?其实我认为至少没有你想的那么可怕。从编程角度来看,这些函数就相当于模块中内置好的方法,只需要调用相应的方法就可以达成想要的目的。而要说难点,首先你要理解你的应用场景,然后根据实际的场景去调用相应的方法,这才是你更应该关注的问题。假设函数和损失函数是机器学习中的两个概念,它并非某个模块下的函数方法,而是我们根据实际应用场景确定的一种函数形式,就像你解决数学的应用题目一样,根据题意写出解决问题的方程组。下面分别来看一下它们的含义。
1) 假设函数
假设函数(Hypothesis Function)可表述为y=f(x)其中 x 表示输入数据,而 y 表示输出的预测结果,而这个结果需要不断的优化才会达到预期的结果,否则会与实际值偏差较大。
2) 损失函数
损失函数(Loss Function)又叫目标函数,简写为 L(x),这里的 x 是假设函数得出的预测结果“y”,如果 L(x) 的返回值越大就表示预测结果与实际偏差越大,越小则证明预测值越来越“逼近”真实值,这才是机器学习最终的目的。因此损失函数就像一个度量尺,让你知道“假设函数”预测结果的优劣,从而做出相应的优化策略。3) 优化方法
“优化方法”可以理解为假设函数和损失函数之间的沟通桥梁。通过 L(x) 可以得知假设函数输出的预测结果与实际值的偏差值,当该值较大时就需要对其做出相应的调整,这个调整的过程叫做“参数优化”,而如何实现优化呢?这也是机器学习过程中的难点。其实为了解决这一问题,数学家们早就给出了相应的解决方案,比如梯度下降、牛顿方与拟牛顿法、共轭梯度法等等。因此我们要做的就是理解并掌握“科学巨人”留下的理论、方法。对于优化方法的选择,我们要根据具体的应用场景来选择应用哪一种最合适,因为每一种方法都有自己的优劣势,所以只有合适的才是最好的。
上述函数的关系图如下所示:
图3:函数关系图
拟合&过拟合&欠拟合
拟合是机器学习中的重要概念,也可以说,机器学习的研究对象就是让模型能更好的拟合数据,那到底如何理解“拟合”这个词呢?1)拟合
形象地说,“拟合”就是把平面坐标系中一系列散落的点,用一条光滑的曲线连接起来,因此拟合也被称为“曲线拟合”。拟合的曲线一般用函数进行表示,但是由于拟合曲线会存在许多种连接方式,因此就会出现多种拟合函数。通过研究、比较确定一条最佳的“曲线”也是机器学习中一个重要的任务。如下图所示,展示一条拟合曲线(蓝色曲线):
图4:曲线拟合
提示:很多和数学相关的编程语言都内置计算拟合曲线的函数,比如 MATLAB 、Python Scipy 等,在后续内容中还会介绍。
2) 过拟合
过拟合(overfitting)与是机器学习模型训练过程中经常遇到的问题,所谓过拟合,通俗来讲就是模型的泛化能力较差,也就是过拟合的模型在训练样本中表现优越,但是在验证数据以及测试数据集中表现不佳。举一个简单的例子,比如你训练一个识别狗狗照片的模型,如果你只用金毛犬的照片训练,那么该模型就只吸纳了金毛狗的相关特征,此时让训练好的模型识别一只“泰迪犬”,那么结果可想而知,该模型会认为“泰迪”不是一条狗。如下图所示:

图5:过拟合
过拟合问题在机器学习中经常原道,主要是因为训练时样本过少,特征值过多导致的,后续还会详细介绍。
3) 欠拟合
欠拟合(underfitting)恰好与过拟合相反,它指的是“曲线”不能很好的“拟合”数据。在训练和测试阶段,欠拟合模型表现均较差,无法输出理想的预测结果。如下图所示:
图6:欠拟合
造成欠拟合的主要原因是由于没有选择好合适的特征值,比如使用一次函数(y=kx+b)去拟合具有对数特征的散落点(y=log2x),示例图如下所示:

图7:欠拟合示例图
欠拟合和过拟合是机器学习中会遇到的问题,这两种情况都不是我期望看到的,因此要避免,关于如何处理类似问题,在后续内容中还会陆续讲解,本节只需要大家熟悉并理解常见的机器学习术语和一些概念即可。
